
函数与极限 1理解函数的概念,掌握函数的表示方法 2会建立简单应用问题中的函数关系式 3了解函数的奇偶性单调性周期性和有界性 4掌握基本初等函数的性质及图形 5理解复合函数及分段函数的有关。
第一章函数与极限 1理解函数的概念,掌握函数的表示方法2会建立简单应用问题中的函数关系式3了解函数的奇偶性单调性周期性和有界性4掌握基本初等函数的性质及图形5理解复合函数及分段函数的有关概念。
高等数学知识点总结 高数大一上期末复习要点 第一章1极限夹逼准则2连续学会用定义证明一个函数连续,判断间断点类型第二章1导数学会用定义证明一个函数是否可导 注连续不一定可导,可导一定连。
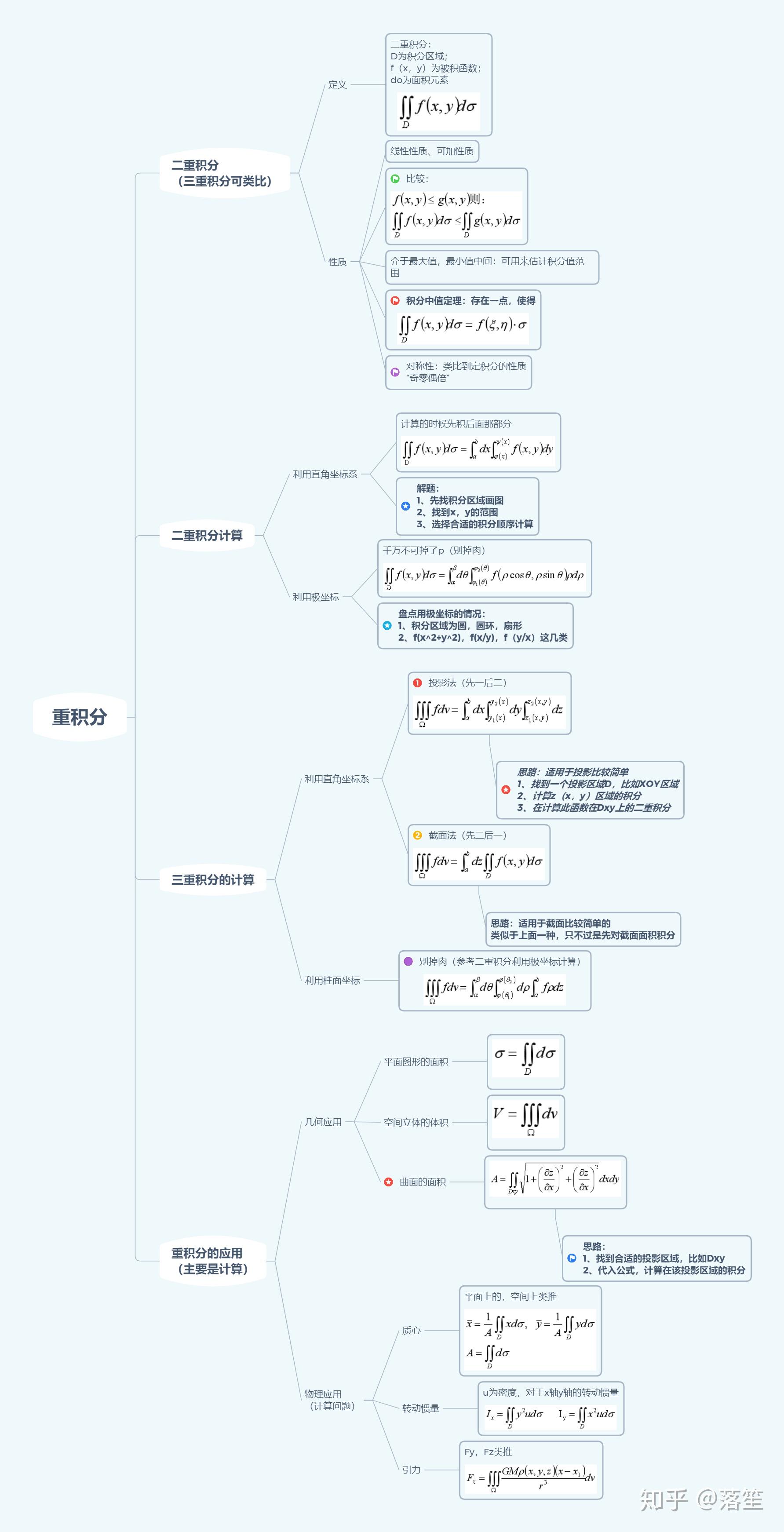
1 夹逼定理的用法 假逼定理是在微积分中最常用到的一种计算方法,它分为函数极限的夹逼定理和数列极限的夹逼定理,如果要正确使用该定理,最重要的是理解夹逼定理是用来计算极限的方法,而不是用来判断是否存在极限的方法。
高等数学微积分是一门非常重要的学科,它涉及到许多复杂的知识点以下是一些可能被认为是困难的微积分知识点1极限与连续理解极限的概念和性质,以及如何计算函数的极限是微积分的基础此外,还需要掌握函数的连续性。
1 知识点定义来源和讲解在高等数学中,abcd通常表示不同的常数或变量它们的具体含义和区别取决于具体的数学问题和上下文 a在代数中,a通常表示一个常数,如a常用于表示一般的实数在函数定义中,a常用。
比如说极限导数等,你要对它们有形象的理解,熟记它们的数学描述,不要只是硬背,可以自己画个图看看,通过多做题,在做题中多多体会学会建立基本框架,总结知识提纲,形成数学思维这些你都能做到了,高等数学应该学得不。
主要的高等数学函数知识,涉及极限的主要有以下几个方面可涉及极限计算的知识点有,连续性及间断点的分类分段函数分段点的连续问题,可导导数是由函数极限来定义的,渐近线,二重极限多元微分学其中,二重极限。
建立知识网络高等数学各个知识点之间有着紧密的联系,要学会建立知识网络将各个知识点联系起来,形成知识体系2做笔记和总结在听课或阅读教材时,应该养成做笔记的习惯记录重要的概念公式和例题,并标注它们之间的。
间断点是我们考研的一个核心知识点,近几年来,间断点的考试频率相对连续而言较大通常出现都是以小题的形式出现,并且得分率并不是非常理想对于找到,找全间断点,并且判断间断点的类型,是同学们需要掌握的一个重要技能。
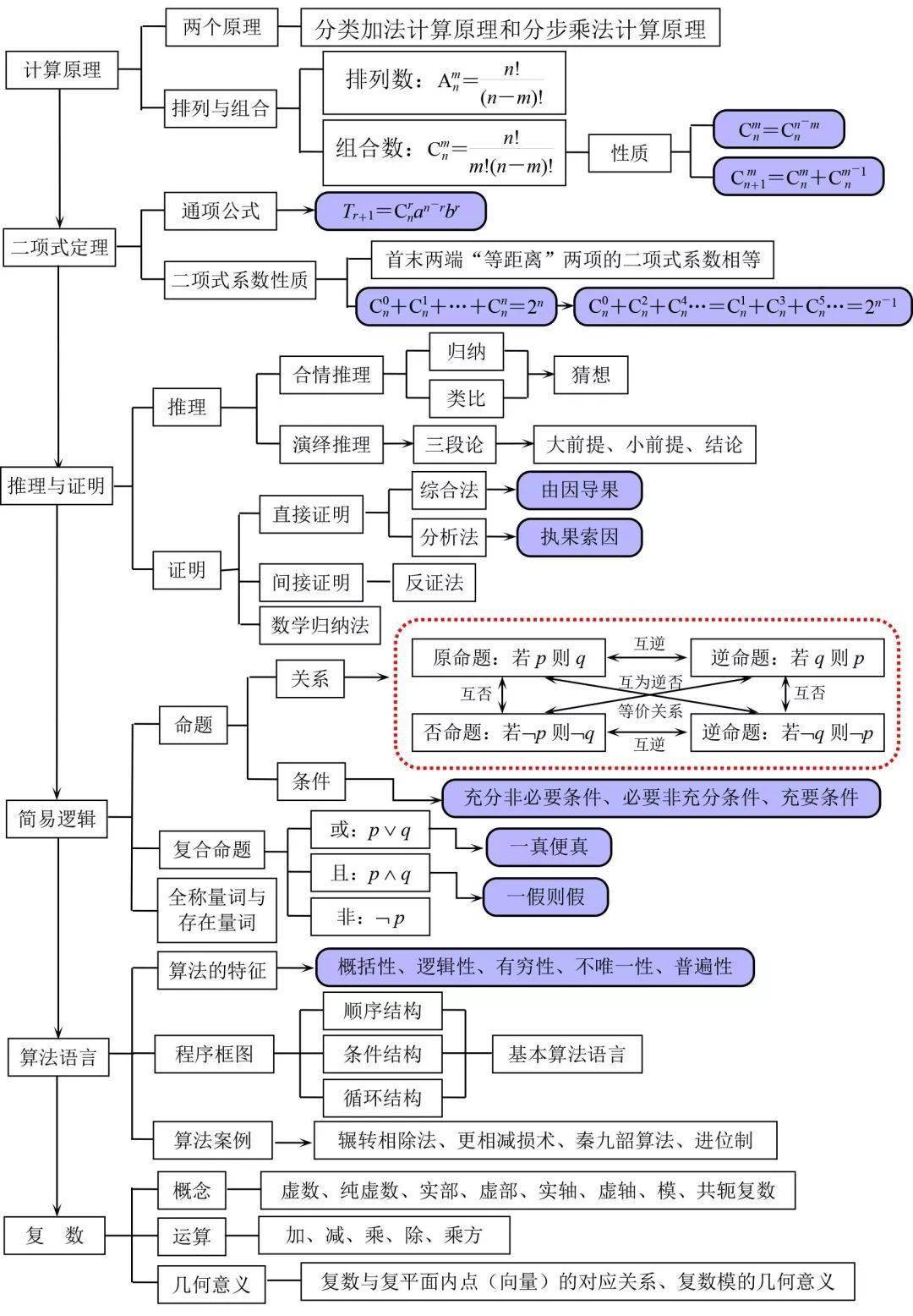
高等数学最重要的就是发散性思维和创新性思维了谈到发散性思维,我想每一个同学都知道,就是通过一个知识点去联想其他知识,谈到导数与微分不定积分积分时,其实它们都是与函数和极限有关的,由最基本的函数与极限到到。
数学是三大公共课中最难的一个部分,复习起来比较吃力,尤其是基础差的考生,而高等数学部分又是数学中最难最重要的,建议2017考生要多放一些经历在重难点上,下面是6个复习重点,大家注意第一求极限无论数学一数学。
区别一主要内容不同高数一主要学数学分析,内容主要为微积分含多元微分重积分及常微分方程和无穷级数等高数二主要学概率统计线性代数等内容区别二主要是对知识的掌握程度要求不同高数一。
微积分的核心知识点是牛顿莱布尼茨公式,又称为微积分基本定理至于你说要这方面习题集,吉米多维数学分析习题集应该是非常好的选择了,一共有6册,中国国内老师编的习题集大部分都是从这套书上来的,因为当年要学习。
只要你善于去归纳总结,你就会发现各个知识点之间的内在联系,找到它们的关键的核心问题 高考数学大题题型总结 一解析几何圆锥曲线 高考解析几何剖析 1很多高考问题都是以平面上的点直线曲线如圆椭圆抛物线双曲线。
第二个13也很好理解,空间坐标点1,1,1关于三个坐标轴投影的余弦值,就是一个单位立方体,对角线长度根号三,边长为1,余弦值根号三除一,平方就是13,三个余弦值之和为1这个知识点可以看高等数学的空间解析几何。
这就需要对自己学的知识加以归纳总结,找出它们之间的内在联系和共同本质的东西,然后使之系统化条理化,从而记住最有代表性的知识点,而其余部分只要在此基础上经过推理便可以了解,这就是“由厚变薄”所以在每章结束或一个单元的内容讲。
标签: #高等数学知识点总结








