
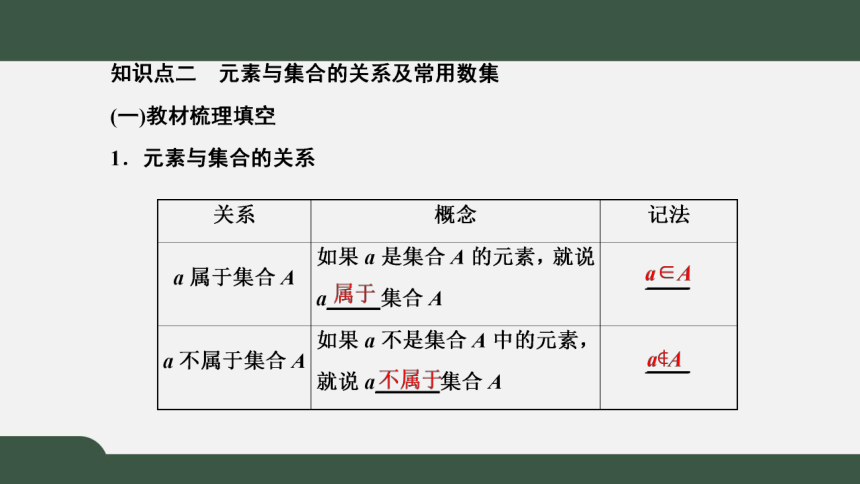
现代数学集合论中,元素是组成集的每个对象换言之,集合由元素组成,组成集合的每个对象被称为组成该集合的元素例如集合1,2,3中 1,2,3都是集合的一个元素元素a与一个给定的集合A只有两种可能1a属于。
集合是一种数学概念,指的是具有特定特征的对象的整体一个集合可以包含任意类型的对象,如数值字母单词图形等集合中的每个对象称为该集合的元素集合用大括号表示,元素在大括号内用逗号分隔二集合的特点。
元素是任何具体或抽象的东西,集合则是由具有某种共同特性或满足某种条件的元素所组成的一个整体元素,也就是数学中所说的对象,可以是任何具体或抽象的东西,如数字字母图形点线面等等它们是构成集合的基本单。
现代数学集合论中,元素是组成集的每个对象集合由元素组成,组成集合的每个对象被称为组成该集合的元素例如集合1,2,3中 1,2,3都是集合的一个元素元素a与一个给定的集合A只有两种可能1a属于集合A。
一个集合可以包含任意数量和类型的元素,从单个元素到无数个元素不等同时,一个元素也可以属于任意数量的集合但是,一个元素只能属于一个集合,不能同时属于两个或更多集合集合和元素的应用1数学领域在数学中。
集合,简称集,是数学中一个基本概念,也是集合论的主要研究对象是由一个或多个确定的元素所构成的整体现代数学集合论中,元素是组成集的每个对象 换言之,集合由元素组成,组成集合的每个对象被称为组成该集合的元素。
高中数学必考知识点归纳大全 1 高一数学 知识点总结集合一集合有关概念 1集合的含义 2集合的中元素的三个特性 1元素的确定性如世界上最高的山 2元素的互异性如由HAPPY的字母组成的集合H,A,P,Y 3元素。
由一个或多个元素所构成的叫做集合,集合是数学中一个基本概念,它是集合论的研究对象,集合是指具有某种特定性质的具体的或抽象的对象汇总成的集体,这些对象称为该集合的元素下面给大家分享一些关于 高一数学 集合知识点 总结 ,希望对。
数学集合符号如下1N非负整数集合或自然数集合0,1,2,3,2N*或N+正整数集合1,2,3,3Z整数集合,1,0,1,4Q有理数集合5Q+正有理数集合6Q负有理数。
集合论的基本理论创立于19世纪,关于集合的最简单的说法就是在朴素集合论最原始的集合论中的定义,即集合是“确定的一堆东西”,集合里的“东西”则称为元素下面我给大家分享一些高中数学集合知识点大全,希望能够帮助。
所以,虽然集合中的概念关系比较多,但只要抓住了元素这个核心概念,集合问题也就迎刃而解如果你对元素的概念还不太理解,下面的课程和练习可以帮助你度过难关高中数学必修1预习课集合的概念与表示2抓住特殊性质互。
由题意,角在第3象限,cos= 根号1sin^2=2根号55。
集合具有某种特定性质的事物的总体这里的“事物”可以是人,物品,也可以是数学元素例如1分散的人或事物聚集到一起使聚集紧急~2数学名词一组具有某种共同性质的数学元素有理数的~3 口号 等等集合在数学概念中。
高中高一数学必修1各章知识点总结 第一章 集合与函数概念 一集合有关概念 1集合的含义某些指定的对象集在一起就成为一个集合,其中每一个对象叫元素 2集合的中元素的三个特性 1元素的确定性 2元素的互异性 3元素。
这些对象可以是数字字母符号等,或者是其他集合集合通常用大写字母表示,且成员间没有重复集合的成员可以是有限个数,也可以是无限个数集合可以用描述法表示,即通过列举集合中的元素或者给出满足某个特定条件的元素。

2 无限集合的元素个数对于无限集合,由于无法直接数出其中的元素个数,可以使用其他方法来确定元素的个数例如,使用数学定义或性质推导出集合的元素个数例如,全体自然数的集合可以用符号N表示,它的元素个数是无穷的。
标签: #高中数学集合和元素








