
懒的用几何画板了,你应该看得懂,如图以BC为边,做正三角形EBC,连接AE 容易证明角AEB=30度 然后容易证明三角形AEB全等于三角形DCB 然后可以得到BD=BA 然后通过角ABD=40度,得到aerfa=70度。
只写思路了哈 1正比例函数y=k1x,反比例函数y=k2\x 设Bp,qDq,p分别带入得出k1=1,k2=1 p和q都消掉了再次带入得出p=1 q=1 得B1,1D1,1BA=1 AO=1 OC=1 CD=1 得ABCD为平行四边形 Sabcd=AB×AC=1×2=2 得四边形ABCD为2 2得E1。
初高中的数学公式定理大集中仅供参考1 过两点有且只有一条直线 2 两点之间线段最短 3 同角或等角的补角相等 4 同角或等角的余角相等 5 过一点有且只有一条直线和已知直线垂直 6 直线外一点与直线上各点连接的所有线段中,垂线段最短 7 平行公理 经过直线外一点,有且只有一条直线与这条直线。
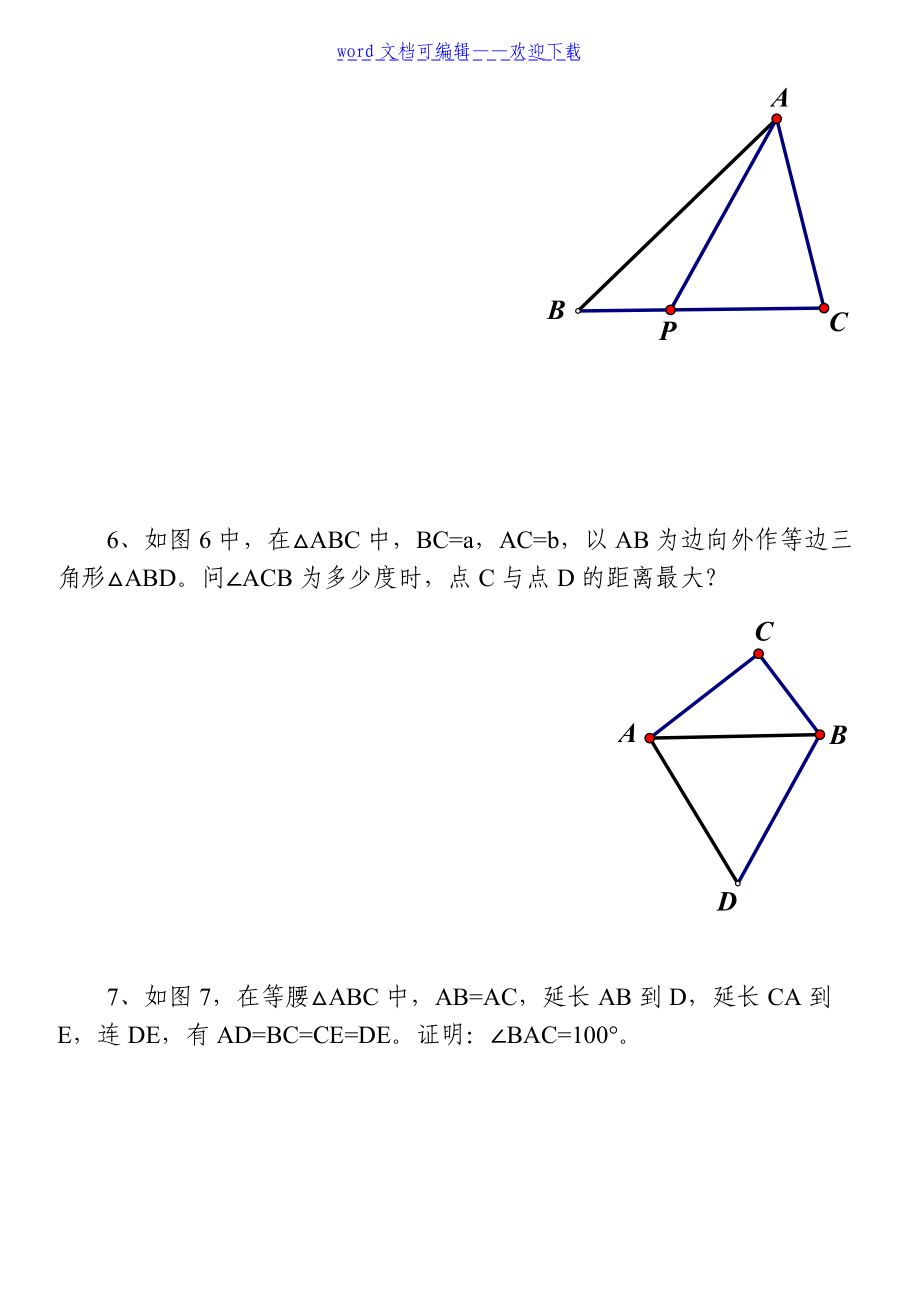
这道题是一次竞赛题选择题中的最后一道,难度肯定是有的,但不同的解题方法,对应的难度也是不一样的该题使用的几何方法确实。
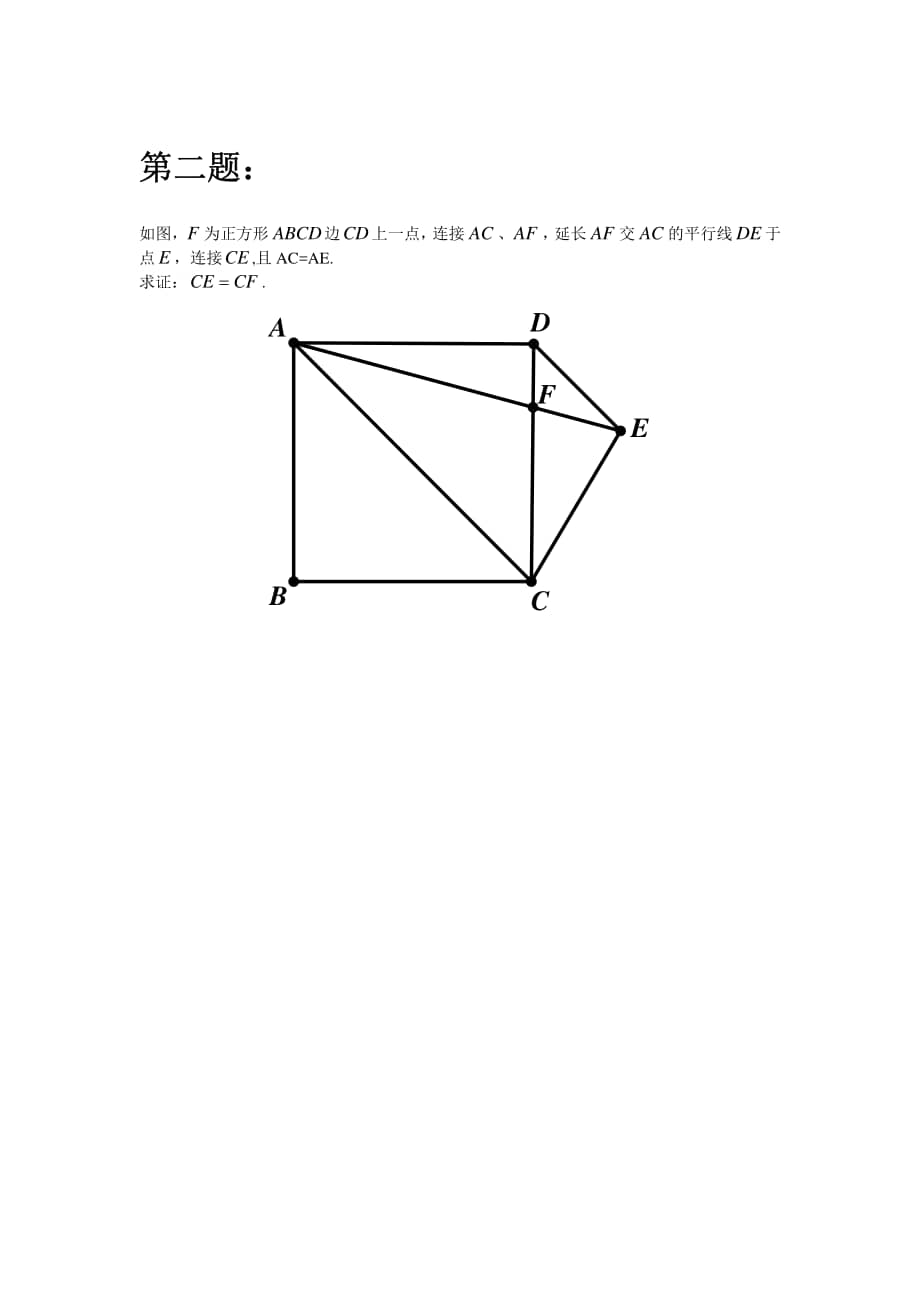
解过点A作AE垂直DB于E交DB度延长线于E,过点A作AF平行EC与过点D作DF平行AE的DF相交于点F,DF与AC相交于点H 所以AEDF是矩形 因为角ADB=45度 角E+角EAD+角ADB=180度 所以角EAD=角ADB=45度 所以AE=DE AD^2=2AE^2 所以AEDF是正方形 所以角F=角E=角BDH=90度 所以设AE=DE=DF=AF=。
过I分别作BI垂直AD于F,AI垂直CD于E首先由I在AD中垂线FB上,所以角IDB=角IAB又AI平分角CAB 所以角IDB=角IAC 所以A,I,O,D四点共圆即DI垂直AE而ID=IA可以知道三角形AFI,三角形IFD,三角形AID都是等腰直角三角形故FI=FD1设MI交CD于P,则若证MPD=90的话,可结合角DFI=90,而去。
”模型 模型二“半角”模型对称半角模型旋转半角模型模型三“角平分线”模。
标签: #初中数学竞赛题几何








